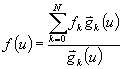Виктор Толстых, Ирина Толстых

Аппроксимация склеивающими функциями

Пусть X – область определения некоторой зависимости F, на которой мы хотим построить аналитическую функцию, аппроксимирующую F.

- функция определенная на X и аппроксимирующая F.

Известно, что согласно теореме Вейерштрасса о полноте полиномов в пространстве непрерывных функций, любуюзависимость можно приблизить, подобрав соответствуюз\щую степень полинома. Фактически же хорошо известно, что подобная аппроксимация выльется в дребезжащую с частотой оцифровки функцию. Таким образом теряется основной смысл аппроксимации – представить зависимость гладкой, «хорошей» функцией, с прогнозом внутренних и внешних точек. Это является причиной, почему так популярны кубические сплайны, удовлетворяющие нашему внутреннему представлению о том какова аппроксимация «должна быть». Разумеетя, это скорее чисто человеческое представление, чем строго формализованное. Но и основной критерий качества аппроксимации часто выступает как именно субъективный типа «нравится-не нравится».

Склеивающие функции позволяют отказаться от безудержного роста локальной сложности зависимости. Любая гладкая зависимость локально хорошо приближается достаточно простыми функциями.

Предположим,что на X задано покрытие открытыми множествами. Выберем подпокрытие индекса 1, с элементами покрытия , ассоциированными с индексированным набором узловых точек , на каждом элементе которого задана аппроксимирующая функция .

Задача склейки заключается в продолжении каждой такой функции с фиксированного значения на всё множество . Причем, на пересечении должно быть равенство .

Гладкое продолжение функций и их производных с бесконечно малой окрестности узла на весь эдемент покрытия назовем гладкой склейкой.

Склеивающей функцией назовем функцию.

По аналогии со сплайн-функциями, наибольший интерес представляют склеивающие функции, непрерывно дифференциируемые на всей области покрытия и сохраняющие значения локальных функций и первые производные в узлах. В одномерном случае такие функции построить несложно. Покажем как это можно сделать.

Локальная сплайн-интерполяция

Для обычных сплайн-методов нам требуется весь интервал данных для одновременных вычислений. Кроме того, мы можем задать фиксированные значения в узлах сетки, но производные задать не можем. Метод достаточно ограничен в своих требованиях.

Кроме того, отрицательным явлением следует считать «дальнодействие» метода – каждая точка интервала влияет на всю кривую. Т.е.локальный всплеск с одного конца отзовется на другом. Локальные сплайны имеют ограниченный радиус действия и вычисляются по ограниченному набору точек.

Рассмотрим на рис.1. интервал [a,b] как множество X, на котором задано двухэлементное покрытие индекса 1, состоящее из интервалов [a,c] и [b,d]. Для этих элементов покрытия выбраны соответствующие узлы на X: b и с. Также на [a,c] и [b,d] заданы две гладких функции f_ac и f_bd, изображенные параболами. На пересечении интервалов для задана склеивающая функци g, плавно переводящая f_ac в f_bd,, а точнее, сводящая обе эти функции внутри интервала к единой f:

на [b,c].

В качестве g может быть выбрана какая угодно функция с требуемыми свойствами. Будь то функция Урысона или даже квадрат синуса. Мы предлагаем воспользоватся замечательной кубической параболой

.

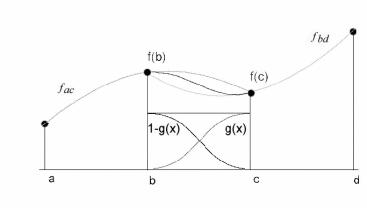
Легко показать, что данная функция является настоящим клеем и гладко(непрерывно-дифференцируемо) склеивает равномерно ограниченные локальные функции, сохраняя в узлах значения локальных функций и их первые производные. Пусть интервалы между узлами равны . Тогда к точке b с двух сторон сходятся четыре склеивающих функции и две локальных функции:
слева

, и ,

справа

, , и .

Тогда функция f принимает равные значения по обе стороны от узла b:

и

Аналогично, с учетом при легко получаем, что производные слева и справа тоже равны:

и .

В частном случае, когда локальные функции заданы обычными параболами, склеенная функция превращается в настоящий обобщенный сплайн класса (5,3), степени 5 и дефекта 3, что внешне мало отличимо от стандартного кубического сплайна класса (3,1). Вместе с тем, нахождение локальных параболических зависимостей на неточно определенных данных «с шумом» легко осуществляется методом наименьших квадратов, что дает один из самых легких и надежных методов аппроксимации одномерных зависимостей произвольной длины.

Многомерная склейка.

Многомерный случай кардинально отличается от одномерного тем, что даже на равномерной сети не удаётся задать разбивающее единицу семейство гладких функций. Вмесе с тем равномерная сеть для многомерных задач – нечто чрезмерное, поскольку количество узлов слишком быстро растет и задача часто становится неудобосчитаемой даже при невысоком уровне детальности. В методах расчета нейронных сетей нашли широкое применение так называемые «мексиканские шляпы»(Mexican Hat), условно разбивающие единицу и произвольно располагающиеся на X для максимально достоверного покрытия наиболее важных участков. Другой путь – симплициальное разбиение компакта X на разумных размеров участки, наиболее полно описывающие поведение искомой звисимости.

Предположим, что у нас имеется симпллициальный комплекс компакта X, подчиненный зависимости F. Тогда задача построения гладкой аппроксимационной зависимости сводится к построению многомерного аналога склеивающей функции g на симплексе.

В принципе, кажется, такая функция строится. Пусть - множество локальных функций, соответствующих узлам N-мерного симплекса и , где - барицентрические координаты симплекса, а g – одномерная склеивающая функция, введенная ранее.

Тогда - единое продолжение каждой локальной функции на весь симплекс со свойствами сохранения локального описания в узлах.

Эта формула пока остаётся недоказанной и непроверенной даже для двумерного случая, хотя частично доказана гладкость её поведение на ребрах и гранях. Также остается недоказанным, что данная склейка корректна для многомерого случая, хотя она является просто обобщенем двумерного случая.