|
В.Н.Толстых Компьютерное
моделирование
топологических
Новая
технология
описания
трехмерных
объектов,
реализованная
в языке
программирования
VRML 2.0 (Virtual Reality Modeling Language)
позволяет
создавать
на экране высококачественные
компьютерные
модели 3-мерных
объектов.
Наибольшее
применение
эта
технология
получила в
области
создания виртуальных
городов и
виртуальных
мест встреч [1] в сети
Интернет.
Для научных
целей она
используется
еще
незначительно.
Вместе с тем одной
из проблем
современной
геометрии и топологии
является
аналитическое
описание и
визуализация
геометрических
объектов. До
появления VRML
многочисленные
технические
трудности
не
позволяли
создать
удобный инструментарий
компьютерного
построения
геометрических
моделей.
Поэтому те
иллюстрации
объектов,
которые нам
приходится
видеть [2][6][7],
сделаны, как
правило,
рукой
художника. В VRML
2.0 некоторые
геометрические
объекты
реализованы
в качестве
геометрических
примитивов (primitive):
Box, Sphere, Conus, Cylinder. Большее
количество этих
объектов может
быть
получено с
использованием
примитивов
3-х мерного
редактора,
лофтинга форм
(loft) и
теоретико-множественных
операций
над этими
примитивами:
объединение,
пересечение,
вычитание. В
целом это
дает
возможность
строить
весьма
впечатляющие
реалистичные
модели,
однако для
построения
даже
простого однополостного
гиперболоида
требуется
много
неавтоматизированной
работы по
вводу
координат. Общее
описание
сложного
объекта-полиэдра
дается
узлом VRML IndexedFaceSet, в
котором
перечисляются
вершины,
ребра и
грани-полигоны
полиэдра, а
также
некоторые
визуальные
характеристики
этих граней,
такие как
цвет,
прозрачность,
нормали
отражающих
плоскостей
и другие.
Ручное
задание
этих
параметров
малопроизводительно,
поэтому они
обычно импортируются
из 3D-редактора.
Более
рационально
эти параметры
получать
прямыми
вычислениями
с помощью
программы
на любом
универсальном
языке
программирования.
На рис. 1
представлены
результаты
работы VRML-программы
в CosmoPlayer 2.0,
динамически
созданной
программой,
написанной
на языке Visual
Basic 5.0.
Рис.1. VRML-модели
однополостного
и
двуполостного
гиперболоидов В
принципе,
любой
алгоритм
построения
полиндрома,
аппроксимирующего
поверхность,
является
алгоритмом
клеточного
или симплициального
разбиения
этой
поверхности
с
сохранением
ориентации.
При этом
возникают
естественные
осложнения,
связанные с
наличием
критических
и особых
точек
поверхности.
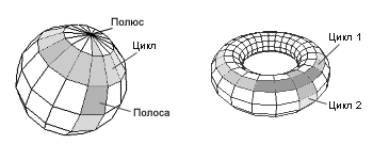
На рис. 2 приведен пример
построения
сферы. В
общем
случае
прямоугольные
клетки
строятся
одна к
другой
вдоль параллелей
по единому
алгоритму.
Такие точки
и клетки их
покрывающие
назовем общими.
Однако
вблизи
полюсов
алгоритм
построения
должен быть
изменен:
либо полюс
закрывается
многоугольником,
либо к
полюсу
сходятся
вершины
треугольных
клеток-симплексов.
Вариант
решения
зависит от
конкретной
реализации
алгоритма,
но общим
является
само наличие
двух точек, в
окрестности
которых алгоритм
построения
изменяется.
Назовем
такие точки особыми
точками
алгоритма
построения. Возникают
естественные
вопросы:
какими
бывают
такие точки,
сколько их,
можно ли
уменьшить
их
количество и как
изменяется
алгоритм
построения
в их
окрестности?
Введем
определения: Индексированным
клеточным
разбиением
поверхности
назовем нумерованную
последовательность
клеток
a1, a2, …
, aN, где
N-общее
число клеток
в полиэдре. Цепью
индексированного
клеточного
разбиения назовем
последовательность
примыкающих
клеток
a1, a2, … , an,
такую, что
любые две
клетки ai, ai+1
с соседними
индексами
имеют общую
сторону. Полосой
назовем
цепь a1, a2, …
, an, каждая
клетка которой
инцидентна
не более чем
двум
соседним
клеткам.
Назовем
полосу регулярной
полосой,
если любая
клетка в ней
не имеет
смежных общих
ребер с
другими
клетками. Циклом
назовем
цепь,
представляющую
замкнутую
полосу, т.е.
полосу,
каждая
клетка
которой
инцидентна
ровно двум
клеткам.
Назовем цикл
регулярным
циклом, если
любая
клетка в нем
не имеет смежных
общих ребер
с другими
клетками .
Теорема
1. Существует
взаимно
однозначное
соответствие
между
индексациями
клеточного
разбиения
замкнутой
ориентируемой
поверхности
Q и
касательными
векторными
полями,
непрерывными
всюду, кроме
конечного
числа точек на
этой поверхности.
Иначе
говоря, для
каждого
алгоритма
построения
найдется
определяющее
его касательное
векторное
поле и
наоборот,
для каждого
касательного
векторного
поля можно
создать
алгоритм
построения
поверхности,
подчиненный
этому полю. Теорема
Хопфа [3]. Если на
замкнутой
ориентируемой
поверхности
Q задано поле
ненулевых
касательных
векторов,
непрерывное
всюду, кроме
конечного
числа особых
точек, то
сумма
индексов
всех особых
точек равна c(Q). Таким
образом,
согласно
теореме Хопфа,
если
ограничиваться
замкнутыми
поверхностями,
то неособые
векторные
поля
существуют
только на
торе. И, по
теореме 1,
алгоритм
построения
без особенностей
возможен
только для
тора. Доказательство
теоремы 1.
Пусть A={ai}-
клеточное
разбиение
поверхности.
С каждой
клеткой ai свяжем
единичное
касательное
вихревое векторное
поле, идущее
по границе
клетки вдоль
ребер в
положительном
направлении
обхода ее
вершин.
Ввиду
односвязности
клетки, поле
может быть
непрерывно
продолжено
внутрь с
наличием
всего
одного
полюса - центра
вихря. Таким
образом
строится
касательное
поле с n
полюсами и c(Q)-n седловыми
точками
поля,
согласно
теореме Хопфа. С
другой
стороны,
пусть P- касательное
векторное
поле с
конечным числом
особых
точек {pi}. Для поля с
невырожденными
особенностями
особыми точками
являются
источники,
стоки,
центры вихрей
и седла.
Вырежем из
поверхности
эти точки
вместе с
небольшими
открытыми
выпуклыми
многоугольниками.
При этом
поле надо немного
сдвинуть,
чтобы оно
обтекало
вырезанные
участки в
районе
седел. Тогда
поле на оставшейся
поверхности
принимает
вид ламинарных
потоков вдоль
которых
можно
производить
клеточное
разбиение
поверхности
на
разомкнутые
регулярные
полосы,
идущие от
источников
к стокам, и
регулярные
циклы,
окружающие
полюса (для
поверхности
с c(Q)=0
существование
циклов
обеспечивает
теорема
Данжуа-Зигеля
[8]).
Таким
образом,
можно
построить
индексацию
клеток,
начиная от
каждой
особой
точки поля. · Из
приведенных
теорем
следует, что минимальное
число
особых
точек
построения
поверхности
Q
определяется
ее
эйлеровой
характеристикой
c(Q).
Известно,
что
замкнутое
ориентируемое
неособое
многообразие
гомеоморфно
сфере с набором
ручек. Добавление
ручки понижает
эйлерову
характеристику
на 2. Поэтому,
начиная со
второй
ручки,
возможно
построение
касательного
векторного
поля
только с
седловыми
точками,
которых
будет
минимальное
число m=2k-2, где
k –
число
ручек. Вопреки ожиданиям, минимизация числа особых точек алгоритма построения не всегда является целесообразным. Рассмотрим пример вклеивания ручки в сферу. В простейшем случае ручка вклеивается в полюса сферы. В этом случае из полюсов убираются заклеивающие их многосторонние клетки, и к ним приклеивается цилиндр с тем же числом сторон. Вопрос о продолжении поля в данном случае решается автоматически.
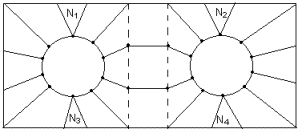
Но таким способом можно вклеить всего одну ручку. В более общем случае следует выбрать прямоугольный участок с ламинарным потоком и заменить его на другой участок с двумя вырезанными полигонами и некоторыми перестроениями в их окрестности, как показано на рис 4 и 5.
Рис.4. Схема перестроения в месте вклеивания ручки с четырьмя «полуседлами» Рис.5. Схема перестроения в месте вклеивания ручки с двумя «седлами»
Мы
полагаем,
что на сфере
уже
существует
индексированное
клеточное
разбиение,
индуцированное
векторным
полем с
двумя
полюсами,
находящимися
вне
выделенного
участка. С
другой стороны,
ручка
топологически
эквивалентна
цилиндру и
векторное
поле на ней
естественным
образом
задается
произведением
S´I. В месте
склейки
ручки мы
должны
обеспечить
склеивание
и векторных
полей. На рис.4
видно, что
построенное
поле имеет
два полюса в
вырезанных
местах и
четыре
«полуседловые»
точки с
полуцелыми
индексами –1/2 (симплексы
N1, N2, N3, N4).
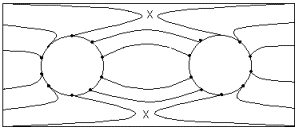
Разумеется,
некоторой
трансформацией
поля четыре
полуседловых
точки можно
свести к
двум
настоящим
седловым точкам X1,
X2, как это
показано на
рис. 5. Однако
это может негативно
сказаться
на
визуальном
качестве
модели
и поэтому в
этом месте
целесообразность
берет верх
над
красотой теории.
Полуседловая
точка может
быть заклеена
отдельным,
не входящим
ни в одну
полосу,
симплексом,
а седловая –
отдельной
клеткой. Классический
способ
построения
векторного
поля с
конечным
числом
особых
точек заключается
в задании на
поверхности
функции
Морса [5],
которая
затем
однозначно
определяет
градиентное
векторное
поле
(вектора касательные
линиям
наискорейшего
спуска). По
теореме
Морса
невыроженные
критические
точки
функции
Морса
однозначно
связаны с
особыми
точками
индуцированного
векторного
поля и
эйлеровой
характеристикой
поверхности
c(Q).
Таким образом,
задание
эффективной
функции Морса
на
поверхности
следует
считать
наиболее
перспективным
приемом в
разработке
алгоритма
построения
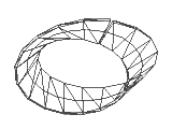
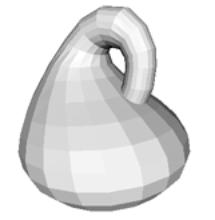
поверхности. Тор
является
топологическим
произведением
двух
окружностей S´S и
его группа
гомологий ZÅZ
имеет два
порождающих
гомологических
цикла C1 и C2,
линейная
комбинация
которых
может стать новым
циклом,
задающим
векторное
поле на торе.
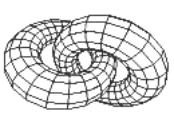
Так цикл 2C1+3C2
заузлен на
торе. Этот
замкнутый
узел известен
под именем
торического
узла,
клеверного
листа или
трехлистника.
Это
указывает
на
принципиальную
возможность
VRML-моделирования
топологических
узлов, используя
кручения
поля на
ручках
сферы [8][9]. Заслуживают отдельного рассмотрения вопросы о построении зацепленных и заузленных поверхностей, многокомпонентных компактных и некомпактных алгебраических поверхностях, а также поверхностей с особенностями.
Рис.7. 3D модель ленты Мебиуса.
Из поверхностей с краем выделяются неориентируемые многообразия. Пример ленты Мебиуса приведен на рис.7. Ввиду односторонности этого объекта, саму полосу следует сразу делать двусторонней либо использовать ее двухстороннее накрытие. Однако первый способ явно проще, поскольку алгоритмически несложно свершить разворот полосы на 180° за полный оборот. Следует только помнить, что в месте склейки направляющая меняет свою ориентацию. На
рис.8
изображено 3D
представление
простейшей
неориентируемой
компактной
поверхности,
известной
как «бутылка
Кляйна».
Построение
велось
горизонтальными
полосами с
последующим
поворотом
плоскости
построения.
В конце построения
была
произведена
инверсная
склейка
первой
полосы с
последней.
Число клеток
в полосе
должно быть
четным.
Следует
отметить,
что наличие
трансверсального
самопересечения
поверхности,
связанное с
невозможностью
ее вложения
в
трехмерное
евклидово
пространство
R3, никак не
отражено в
алгоритме
построения и
для этого
даже не
пришлось
вырезать
дыру в боку
бутылки.
Теория
построения
неориентируемых
поверхностей
в данной
работе не
рассматривается.
Однако само
построение обладает
замечательной
особенностью
порождать
каноническое
двулистное
накрытие r такой
поверхности
X,
при котором
само
накрывающее
многообразие
Y является
ориентируемым,
внешне
ничем не
отличаясь
от
накрываемого
r:Y®X.
Множество
вершин Y
совпадает с
множеством
вершин X, но
грани в VRML-описании
накрывающего
многообразия
даются
дважды: с
прямым и
инверсным
перечислением
вершин,
меняющим
ориентацию
грани. Таким образом,
можно не
заботиться
об
инверсном склеивании
краев в
месте
стыковки и
обеспечении
исходной
двусторонности
поверхности,
а
продолжить
построение
до
следующей
стыковки. В
случае с
«бутылкой
Кляйна» такое
накрывающее
многообразие
топологически
эквивалентно
тору, дважды
ее
обертывающему. В
заключение
отметим, что
для обеспечения
гладкости
геометрических
поверхностей
не требуется
бесконечного
дробления
модели на
мелкие
полигоны. В
последних
версиях VRML-броузеров
реализован
узел Normal, позволяющий
задавать
гладкое
поле нормалей
отражающих
поверхностей
на множестве
граней
полиэдра.
Таким
образом, мы
можем добиться
прекрасных
визуальных
характеристик
поверхностей
при
относительно
небольшом
числе аппроксимирующих
полигонов. Литература 1. V.N.Tolstykh,
I.V.Shturz. Creating large optimized VRML worlds. International Workshop on New Approaches to High-Tech Materials.
Vol.3687, 1999. 2. А.Т.Фоменко,
Д.Б.Фукс. Курс
гомотопической
топологии. М,1989 3.
Б.А.Дубровин,
С.В.Новиков,
А.Т.Фоменко.
Современная
геометрия, М,
1979 4. В.И.Арнольд,
А.Н.Варченко,
С.М.Гуссейн-Заде.
Особенности
дифференцируемых
отображений.
М,1982. 5.
М.М.Постников.
Введение в
теорию
Морса. М, 1971. 6. Д.Гильберт,
С.Кон-Фоссен.
Наглядная
геометрия.
М,1981. 7.
В.Г.Болтянский,
В.А.Ефремович.
Наглядная
топология. М,
1982. 8. И.Тамура.
Топология
слоений. М, 1979. 9. Р.Кроуэлл,
Р.Фокс.
Введение в
теорию
узлов. М,1967. 10.
Ф.Препарата,
М.Шеймос.
Вычислительная
геометрия:
Введение. М, 1989. |